已知 为复数,
为复数, 为纯虚数,
为纯虚数, ,且
,且 ,求复数
,求复数 .
.
已知命题
①函数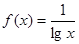 在
在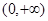 上是减函数;
上是减函数;
②函数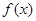 的定义域为R,
的定义域为R,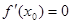 是
是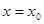 为极值点的既不充分也不必要条件;
为极值点的既不充分也不必要条件;
③函数 的最小正周期为
的最小正周期为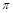 ;
;
④在平面内,到定点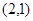 的距离与到定直线
的距离与到定直线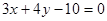 的距离相等的点的轨迹是抛物线;
的距离相等的点的轨迹是抛物线;
⑤已知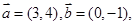 则
则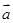 在
在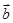 方向上的投影为
方向上的投影为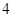 。
。
其中,正确命题的序号是。(把你认为正确命题的序号都填上)
已知数列{an}是等差数列,数列{bn}是等比数列,且对任意的n∈N*,都有a1b1+a2b2+a3b3+···+anbn=n·2n+3.
(1)若{bn}的首项为4,公比为2,求数列{an+bn}的前n项和Sn;
(2)若a1=8.
①求数列{an}与{bn}的通项公式;
②试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它r(r∈N,r≥2)项的和?若存在,请求出该项;若不存在,请说明理由.
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别写出用x表示y和S的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
已知{an}是公比为q的等比数列,且am、am+2、am+1成等差数列.
(1)求q的值;
(2)设数列{an}的前n项和为Sn,试判断Sm、Sm+2、Sm+1是否成等差数列?并说明理由.
已知圆的内接四边形ABCD的边长分别为AB=2,BC=6, CD=DA=4,
(1)求角A的大小;
(2)求四边形ABCD的面积.