已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
①构造一个真命题,画图并给出证明;
②构造一个假命题,举反例加以说明.
如图,在等腰梯形ABCD中,AD∥BC,AC平分∠BCD,已知AD=5cm,BC=9cm,
求等腰梯形ABCD的周长.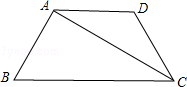
如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE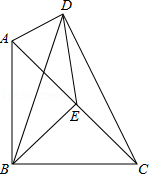
(1)若AC=10,BD=8,求△BDE的周长;
(2)判断△BDE的形状,并说明理由.
已知:如图,在△ABC中,CD⊥AB垂足为D,BE⊥AC垂足为E,连接DE,点G、F分别是BC、DE的中点.
求证:GF⊥DE.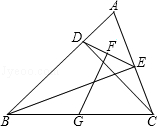
如图,已知△ABC是等边三角形,BD是△ABC的中线,延长BC至E,使CE=CD,连接DE,试说明BD=ED的理由.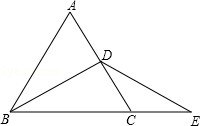
如图,BD是等边△ABC的高,E是BC延长线上一点,且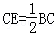 .
.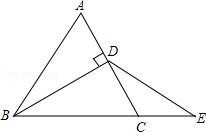
(1)直接写出CE与CD的数量关系;
(2)试说明△BDE是等腰三角形.