在平面直角坐标系 中,点P到两点(0,-
中,点P到两点(0,-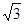 )、(0,
)、(0,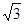 )的距离之和等于4.设点P的轨迹为C.
)的距离之和等于4.设点P的轨迹为C.
(1)写出C的方程;
(2)设直线y=kx+1与C交于A、B两点.k为何值时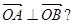 此时|
此时|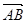 |的值是多少?
|的值是多少?
从一箱产品中随机地抽取一件产品,设事件A为“抽到一等品”,事件B为“抽到二等品”,事件C为“抽到三等品”,且已知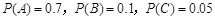 .求下列事件的概率:
.求下列事件的概率:
(1)事件D“抽到的是一等品或二等品”;
(2)事件E“抽到的是二等品或三等品”.
假设人的某一特征(如眼睛大小)是由他的一对基因所决定的,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人是纯隐性,具有rd基因的人为混合性.纯显性与混合性的人都表露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性.
问:(1)一个孩子有显性基因决定的特征的概率是多少?
(2)两个孩子中至少有一个有显性基因决定的特征的概率是多少?
甲、乙两选手在同样条件下击中目标的概率分别为0.4与0.5(这里击中与否互不影响对方),则命题:“至少有一人击中目标的概率为P=0.4+0.5=0.9”正确吗?为什么?(这里只需要能回答为什么即可,而不需要指出概率的大小)
某班学生在一次数学考试中数学成绩的分布如下表:
| 分数段 |
[0,80) |
[80,90) |
[90,100) |
[100,110) |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
| 人数 |
2 |
5 |
6 |
8 |
12 |
6 |
4 |
2 |
求(1)分数在[100,110)中的概率;
(2)分数不满110分的概率.(精确到0.01)
某射手在一次射击中,击中10环、9环、8环的概率分别是0.24、0.28、0.19,求这个射手在一次射击中:
(1)击中10环或9环的概率;
(2)小于8环的概率.