某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其重量(单位:克)是否合格,分别记录了6个抽查数据,获得重量数据的茎叶图如图4.
(1)根据样品数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对较稳定;
(2)若从乙车间6件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过2克的概率.
本小题满分12分)
已知函数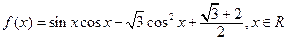
(1)求函数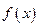 的最小正周期及函数取最小值时自变量
的最小正周期及函数取最小值时自变量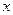 的集合
的集合
(2)确定函数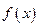 的单调递增区间
的单调递增区间
(3)若函数y=sin2x的图象向右平移m个单位(|m|<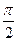 ),向上平移n个单位后得到函数y=f(x)的图象,求实数m、n的值
),向上平移n个单位后得到函数y=f(x)的图象,求实数m、n的值
(本小题满分10分)
已知向量: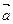 =(cos
=(cos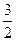 x,sin
x,sin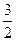 x),
x),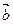 =(cos
=(cos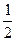 x,-sin
x,-sin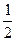 x),且x∈[
x),且x∈[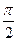 ,π]
,π]
(1)求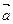 ·
·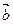 ,|
,|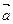 +
+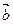 |
|
(2)求f(x)=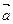 ·
·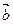 +2|
+2|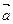 +
+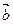 |的最小值
|的最小值
(本小题满分8分)
如图,在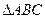 中,D、E分别是AB、AC的中点,DM=
中,D、E分别是AB、AC的中点,DM=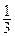 DE,若
DE,若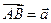 ,
,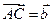
(1)用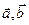 表示
表示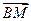
(2)若N为线段BC上的点,且BN=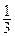 BC,用向量方法证明:A、M、N三点共线
BC,用向量方法证明:A、M、N三点共线
(本小题满分10分
已知 =(1,2),
=(1,2),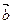 =(x,1),分别求x的值使
=(x,1),分别求x的值使
①(2 +
+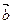 )⊥(
)⊥( -2
-2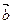 );②(2
);②(2 +
+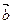 )∥(
)∥( -2
-2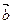 );③
);③ 与
与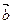 的夹角是600
的夹角是600
(本小题满分14分)
椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
⑴求椭圆方程;
⑵求m的取值范围.