设函数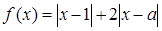 ,
,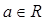 .
.
(1)当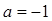 时,求不等式
时,求不等式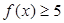 的解集;
的解集;
(2)若不等式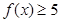 对
对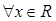 恒成立,求实数
恒成立,求实数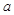 的取值范围.
的取值范围.
(本小题满分12分)
在直角坐标系中,一运动物体经过点A(0,9),其轨迹方程为y=ax2+c(a<0),D=(6,7)为x轴上的给定区间。
(1)为使物体落在D内,求a的取值范围;
(2)若物体运动时又经过点P(2,8.1),问它能否落在D内?并说明理由。
(本小题满分12分)
已知函数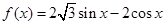 。
。
(1)若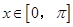 ,求
,求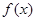 的最大值和最小值;
的最大值和最小值;
(2)若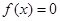 ,求
,求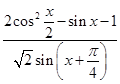 的值。
的值。
(本小题满分13分)
设函数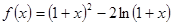 。
。
(1)求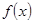 的单调区间;
的单调区间;
(2)若当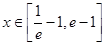 时,(其中
时,(其中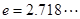 )不等式
)不等式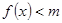 恒成立,求实数
恒成立,求实数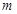 的取值范围;
的取值范围;
(3)试讨论关于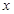 的方程:
的方程: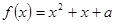 在区间
在区间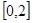 上的根的个数。
上的根的个数。
(本小题满分14分)
已知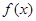 是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:
是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足: 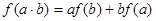 。
。
(1)求f(0),f(1)的值;
(2)判断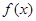 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(3)若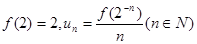 ,求数列{un}的前n项的和Sn 。
,求数列{un}的前n项的和Sn 。
((本题满分14分)某射手每次射击击中目标的概率是,且各次射击的结果互不影响。
(1)假设这名射手射击5次,求恰有2次击中目标的概率;
(2)假设这名射手射击5次,求有3次连续击中目标,另外2次未击中目标的概率;
(3)假设这名射手射击3次,每次射击,击中目标得1分,未击中目标得0分.在3次射击中,若有2次连续击中,而另外1次未击中,则额外加1分;若3次全击中,则额外加3分.记ξ为射手射击3次后的总得分数,求ξ的分布列.