额定功率是80kW的无轨电车,其最大速度是72km/h,质量是2t,如果它从静止先以2m/s2的加速度匀加速开出,阻力大小一定,则:
(1)电车匀加速运动行驶能维持多少时间?
(2)又知电车从静止驶出到增至最大速度共经历了21s,在此过程中,电车通过的位移是多少?
如图所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点。水平桌面右侧有一竖直放置的光滑轨道MNP,其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧,MN为其竖直直径,P点到桌面的竖直距离也是R。用质量m1=0.4kg的物块将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点。用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放,物块过B点后其位移与时间的关系为 ,物块飞离桌面后由P点沿切线落入圆轨道。g=10m/s2,求:
,物块飞离桌面后由P点沿切线落入圆轨道。g=10m/s2,求:
⑴BP间的水平距离。
⑵判断m2能否沿圆轨道到达M点
⑶释放后m2运动过程中克服摩擦力做的功
如图所示,无动力传送带水平放置,传送带的质量M=4kg,长L=5m,轮与轴间的摩擦及轮的质量均不计。质量为m=2kg的工件从光滑弧面上高为h=0.45m的a点由静止开始下滑,到b点又滑上静止的传送带,工件与皮带之间的动摩擦因数 ,
,
求
⑴工件离开传送带时的速度
⑵工件在传送带上运动时的时间
⑶系统损失的机械能
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计粒子所受重力).在该区域AB边的中点处由静止释放电子,求:
(1)电子进入电场II时的速度?
(2)电子离开ABCD区域的位置?
(3)电子从释放开始到离开电场II过程中所经历的时间?
(12分) 如图所示,电阻R1=8Ω,电动机内绕线电阻R0=2Ω。当开关S闭合,S1断开时,电阻R1消耗的电功率为2.88W;当开关S、S1都闭合时,电阻R1消耗的电功率是2W,若电源的电动势为6V。求开关S、S1都闭合时电动机输出的机械功率是多少?电源内阻是多少?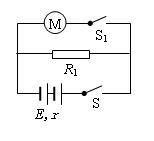
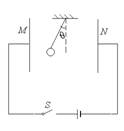
如图所示的装置中,平行板电场中有一质量为m,带电量为q的小球,用长L的细线拴住后在电场中处于平衡位置,此时线与竖直方向的夹角为θ,两板间的距离为d,求:
(1)小球带何种电荷?
(2)两板间的电势差是多少?
(3)把线拉成竖直向下的位置,放手后小球到达平衡位置时的速度为多大?