如图，抛物线y=ax2+bx+c（a，b，c是常数，a≠0）的对称轴为y轴，且经过（0，0）和（
，
）两点，点P在该抛物线上运动，以点P为圆心的⊙P总经过定点A（0，2）．
（1）求a，b，c的值；
（2）求证：在点P运动的过程中，⊙P始终与x轴相交；
（3）设⊙P与x轴相交于M（x1，0），N（x2，0）（x1＜x2）两点，当△AMN为等腰三角形时，求圆心P的纵坐标．
如图，所有小正方形的边长都为1，A、B、C都在格点上．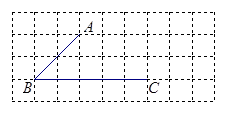
（1）过点C画直线AB的平行线(不写作法，下同)；
（2）过点A画直线BC的垂线，并注明垂足为G；
过点A画直线AB的垂线，交BC于点H.
（3）线段 的长度是点A到直线BC的距离，线段AH的长度是点到直线 的距离.
（4）因为直线外一点到直线上各点连接的所有线中，垂线段最短，所以线段AG、AH的大小关系为AGAH.
先化简，再求值：
2x2＋(－x2－2xy＋2y2)－3(x2－xy＋2y2)，其中x＝2，y＝－．
解关于x的方程:（1）
（2）
计算（1）
（2）
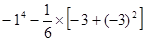
一天，小红与小丽利用温差测量山的高度，小红在山顶测得温度是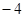
℃，小丽此时在山脚测得温度是6℃.已知该地区高度每增加100米，气温大约降低
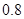℃，这个山峰的高度大约是多少米？