在△ABC和△DEF中,∠C=∠F=90°.有如下五张背面完全相同的纸牌①、②、③、④、⑤,其正面分别写有五个不同的等式,小民将这五张纸牌背面朝上洗匀后先随机摸出一张(不放回),再随机摸出一张.请结合以上条件,解答下列问题.
(1)、你认为 和 组合,△ABC和△DEF不一定全等,
(2)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用①、②、③、④、⑤表示);
(3)用两次摸牌的结果和∠C=∠F=90°作为条件,求能满足△ABC和△DEF全等的概率.
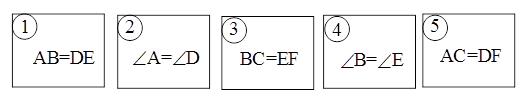
当a取某一范围内的实数时,代数式 的值是一个常数(确定的值),请找出这个范围.
的值是一个常数(确定的值),请找出这个范围.
某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN.
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
【改编题】10分(2013菏泽)如图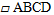 中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,
中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,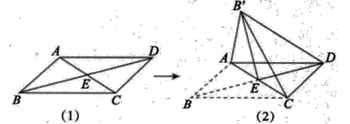
(1)将△ABC沿AC所在直线翻折90°到其原来所在的同一平面内,若点B的落点记为B′,如图(2)所示,求DB′的长;
(2)当将△ABC沿AC所在直线翻折60°时,能否求出线段DB′的长?如果能,求出长度,如果不能说明理由.
8分,在一块边长为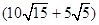 m的正方形土地中,修建了一个边长为
m的正方形土地中,修建了一个边长为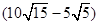 m的正方形养鱼池,问:剩余部分的面积是多少?
m的正方形养鱼池,问:剩余部分的面积是多少?
12分,如图,在▱ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,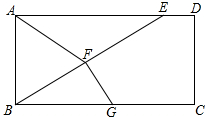
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.