为美化青岛,创建文明城市,园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配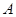 、
、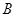 两种园艺造型共50个,摆放在迎宾大道两侧.搭配每个造型所需花卉情况如右表所示:
两种园艺造型共50个,摆放在迎宾大道两侧.搭配每个造型所需花卉情况如右表所示: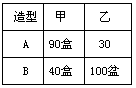
结合上述信息,解答下列问题:
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个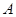 种造型的成本为1000元,搭配一个
种造型的成本为1000元,搭配一个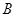 种造型的成本为1200元,试说明选用(1)中哪种方案成本最低?
种造型的成本为1200元,试说明选用(1)中哪种方案成本最低?
南宁市是广西最大的罗非鱼养殖产区,被国家农业部列为罗非鱼养殖优势区域.某养殖场计划下半年养殖无公害标准化罗非鱼和草鱼,要求这两个品种总产量 (吨)满足:
(吨)满足: ,总产值为1000万元.已知相关数据如右表所示.
,总产值为1000万元.已知相关数据如右表所示.
| 品种 |
单价(万元/吨) |
| 罗非鱼 |
0.45 |
| 草鱼 |
0.85 |
求:该养殖场下半年罗非鱼的产量应控制在什么范围?(产值=产量 单价)
单价)
解不等式组: 并将解集在数轴上表示出来.
并将解集在数轴上表示出来.
解不等式组:
某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2 090万元,但不超过2 096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
| A |
B |
|
| 成本(万元/套) |
25 |
28 |
| 售价(万元/套) |
30 |
34 |
(1)该公司对这两种户型住房有哪几种建房方案?
(2)该公司如何建房获得利润最大?
(3)根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?(注:利润 售价
售价 成本)
成本)