有一玻璃半球，右侧面镀银，光源S就在其对称轴SO上（O为球心），且SO水平，如右图所示。从光源S发出的一束光射到球面上，其中一部分光经球面反射后恰能竖直向上传播，另一部分光折入玻璃半球内，经右侧镀银面第一次反射恰能沿原路返回。若球面半径为R，玻璃折射率为
，求光源S与球心O之间的距离SO为多大？
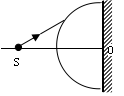
将一个物体以20m/s速度从20m的高度水平抛出，落地时它的速度方向与水平地面的夹角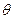
是多少？（不计空气阻力，取
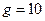m/s2）
如图所示，在水平地面上固定一倾角θ=37°，表面光滑的斜面体，物体A以v1=6m/s的初速度沿
斜面上滑，同时在物体A的正上方，有一物体B以某一初速度水平抛出。如果当A上滑到最高点时恰好被B物
体击中。（A、B均可看作质点， sin37°=0.6，cos37°=0.8，g取10
m/s2）求：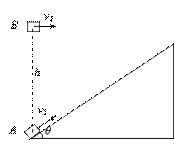
（1）物体A上滑到最高点所用的时间t；
（2）物体B抛出时的初速度v2；
（3）物体A、B间初始位置的高度差h。
如图所示，将一根光滑的细金属折成V形，顶角为
，其对称轴竖直，在其中一边套上一个质量为m的小金属环P．
（1）若固定V形细金属棒，小金属环P从距离顶点O为x的A点处由静止开始自由滑下，则小金属环由静止下滑
至顶点O点时需多长时间?
（2）
若小金属环P随V形细金属棒绕其对称轴以每秒n转匀速转动，则小金属环离对称轴的距离为多少?
如图所示，排球网高为H，半场长为L，运动员扣球点高为h，扣球点离网水平距离为s。若运动员扣出的球水平飞出，且落在对方半场内，不计空气阻力，求：运动员扣球速度的取值范围。
从某一高度平抛一物体，当抛出2s后它的速度方向与水平方向成45°角，落地时速度方向与水平成60°角，g取10m/s2。求：
（1）抛出时的初速度；
（2）落地时的速度；
（3）抛出点距地面的高度；
（4）水平射程。