(1)在图1中,平行四边形ABCD的顶点A,B,C,D的坐标(如图),请写出图中的顶点C的坐标( _________ , _________ ).
(2)在图2中,平行四边形ABCD的顶点A,B,C,D的坐标(如图),求出图中的标点C的坐标,并说明理由(C点坐标用含c,d,e的代数式表示).
归纳与发现
(3)通过对图1,2的观察,你会发现:图3中的平行四边形ABCD的顶点坐标为A(a,b),B(c,d),C(m,n),D(e,f)时,则横坐标a,c,m,e之间的等量关系为 _________ .
如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点B,且OA = 3,AB = 5.点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AO返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BO-OP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).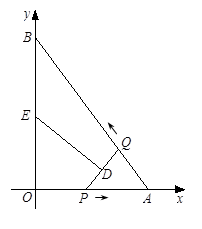
(1)求直线AB的解析式;
(2)在点P从O向A运动的过程中,求△APQ的面积S与t之间的函数关系式(不必写出t的取值范围);
(3)在点E从B向O运动的过程中,完成下面问题:
①四边形QBED能否成为直角梯形?若能,请求出t的值;若不能,请说明理由;
②当DE经过点O时,请你直接写出t的值.
如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按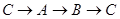 的路径运动,且速度为每秒1㎝,设出发的时间为t秒.
的路径运动,且速度为每秒1㎝,设出发的时间为t秒.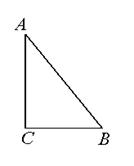
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按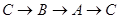 的路径运动,且速度为每秒2㎝,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?(其中(3)直接写出答案即可)
的路径运动,且速度为每秒2㎝,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?(其中(3)直接写出答案即可)
如图,等边 中,D是AB边上的动点,以CD为一边,向上作等边
中,D是AB边上的动点,以CD为一边,向上作等边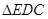 ,连结AE。
,连结AE。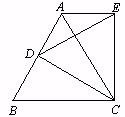
(1)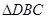 和
和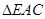 会全等吗?请说说你的理由。
会全等吗?请说说你的理由。
(2)试说明AE∥BC的理由.
在同一平面内,如果有两条直线都与第三条直线垂直,那么这两条直线的位置关系是。(填“垂直”或“平行”)