如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC、CD上如何滑动,总有BE=CF;
(2)当点E、F在BC、CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.
(1)如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
(2)植树节期间,两所学校共植树834棵,其中海石中学植树的数量比励东中学的2倍少3棵,两校各植树多少棵?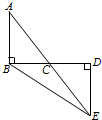
已知:在△ABC中,BC=2AC,∠DBC=∠ACB,BD=BC,CD交线段AB于点E.
(1)如图l,当∠ACB=900时,则线段DE、CE之间的数量关系为
(2)如图2,当∠ACB=1200时,求证:DE=3CE:
(3)如图3,在(2)的条件下,点F是BC边的中点,连接DF,DF与AB交于G,△DKG和△DBG关于直线DG对 称(点B的对称点是点K,延长DK交AB于点H.若BH=10,求CE的长
称(点B的对称点是点K,延长DK交AB于点H.若BH=10,求CE的长


在平面直角坐标系中,点0是坐标原点,四边形ABCD为菱形,AB边在x轴上,点D在y轴上,点A的坐标是(一6,0),AB=10.
(1)求点C的坐标:
(2)连接BD,点P是线段CD上一动点(点P不与C、D两点重合),过点P作PE∥BC交BD与点E,过点B作BQ⊥PE交PE的延长线于点Q.设PC的长为x,PQ的长为y,求y与x之间的函数关系式(直接写出自变量x的取值范围);
(3)在(2)的条件下,连接AQ、AE,当x为何值时,S△BOE+S△AQE= S△DEP并判断此时以点P为圆心,以5为半径的⊙P与直线BC的位置关系,请说明理由.
S△DEP并判断此时以点P为圆心,以5为半径的⊙P与直线BC的位置关系,请说明理由.
义洁中学计划从荣威公司购买A、B两种型号的小黑板,经洽谈,购买一块A型小黑板比买一块B型小黑板多用20 元.且购买5块A型小黑板和4块B型小黑板共需820元.
元.且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需要多少元?
(2)根据义洁中学实际情况,需从荣威公司购买A、B两种型号的小黑板共60块,要求购买A、B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的 .请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案?
.请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案?
哈市某中学为了丰富校园文化生活.校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查。将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
(1)通过计算补全条形统计图;
(2)在这次调查中,一共抽取了多少名学生?
(3)如果全校有680名学生,请你估计这680名学生中参加演讲比赛的学生有多少名?