巴西世界杯足球赛正在如火如荼进行.某人为了了解我校学生“通过电视收看世界杯”是否与性别有关,从全校学生中随机抽取30名学生进行了问卷调查,得到了如下列联表:
| |
男生 |
女生 |
合计 |
| 收看 |
10 |
|
|
| 不收看 |
|
8 |
|
| 合计 |
|
|
30 |
已知在这30名同学中随机抽取1人,抽到“通过电视收看世界杯”的学生的概率是 .
.
(I)请将上面的列联表补充完整,并据此资料分析“通过电视收看世界杯”与性别是否有关?
(II)若从这30名同学中的男同学中随机抽取2人参加一活动,记“通过电视收看世界杯”的人数为X,求X的分布列和均值.
  |
0.100 |
0.050 |
0.010 |
 |
2.706 |
3.841 |
6.635 |
(参考公式: ,
,  )
)
如图,已知正方形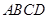 的边长为
的边长为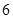 ,点
,点 分别在边
分别在边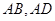 上,
上, ,现将△
,现将△ 沿线段
沿线段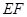 折起到△
折起到△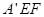 位置,使得
位置,使得 .
.
(1)求五棱锥 的体积;
的体积;
(2)求平面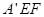 与平面
与平面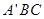 的夹角.
的夹角.
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于 小于
小于 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 |
 |
 |
 |
 |
 |
 |
| 甲 |
3 |
7 |
20 |
40 |
20 |
10 |
| 乙 |
5 |
15 |
35 |
35 |
7 |
3 |
现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算新工人乙生产三件产品A,给工厂带来盈利大于或等于100元的概率;
(2)记甲乙分别生产一件产品A给工厂带来的盈利和记为X,求随机变量X的概率分布和数学期望.
已知公比不为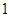 的等比数列
的等比数列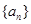 的首项
的首项 ,前
,前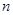 项和为
项和为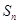 ,且
,且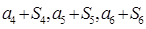 成等差数列.
成等差数列.
(1)求等比数列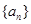 的通项公式;
的通项公式;
(2)对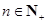 ,在
,在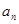 与
与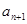 之间插入
之间插入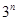 个数,使这
个数,使这 个数成等差数列,记插入的这
个数成等差数列,记插入的这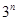 个数的和为
个数的和为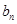 ,求数列
,求数列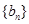 的前
的前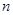 项和
项和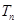 .
.
已知二项式 的展开式中第2项为常数项
的展开式中第2项为常数项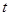 ,其中
,其中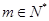 ,且展开式按
,且展开式按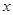 的降幂排列.
的降幂排列.
(1)求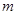 及
及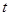 的值.
的值.
(2)数列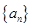 中,
中, ,
,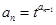 ,
,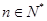 ,求证:
,求证: 能被4整除.
能被4整除.
如图, 是直角梯形,∠
是直角梯形,∠ =90°,
=90°, ∥
∥ ,
, =1,
=1, =2,又
=2,又 =1,∠
=1,∠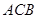 =120°,
=120°,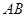 ⊥
⊥ ,直线
,直线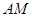 与直线
与直线 所成的角为60°.
所成的角为60°.
(1)求二面角 的的余弦值;
的的余弦值;
(2)求点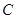 到面
到面 的距离.
的距离.