已知抛物线 .
.
(1)若直线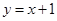 与抛物线
与抛物线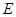 相交于
相交于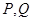 两点,求
两点,求 弦长;
弦长;
(2)已知△ 的三个顶点在抛物线
的三个顶点在抛物线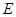 上运动.若点
上运动.若点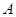 在坐标原点,
在坐标原点,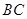 边过定点
边过定点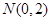 ,点
,点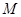 在
在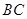 上且
上且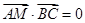 ,求点
,求点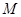 的轨迹方程.
的轨迹方程.
已知函数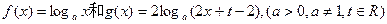 的图象在x=2处的切线互相平行.
的图象在x=2处的切线互相平行.
(1)求t的值.
(2)设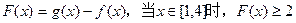 恒成立,求a的取值范围.
恒成立,求a的取值范围.
已知函数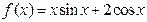 的定义域为
的定义域为 。
。
(1)求证:直线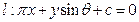 (其中
(其中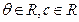 )不是函数
)不是函数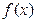 图像的切线;
图像的切线;
(2)判断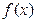 在
在 上单调性,并证明;
上单调性,并证明;
(3)已知常数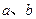 满足
满足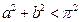 ,求关于
,求关于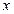 的不等式
的不等式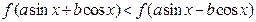 的解集
的解集
已知函数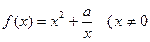 ,常数
,常数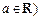 .
.
(1)当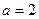 时,解不等式
时,解不等式 ;
;
(2)讨论函数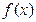 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(3)(理做文不做)若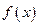 在
在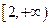 是增函数,求实数
是增函数,求实数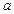 的范围
的范围
已知函数f(x)=ax3+x2-x (a∈R且a≠0) (1)若函数f(x)在(2,+∞)上存在单调递增区间,求a的取值范围.
(1)若函数f(x)在(2,+∞)上存在单调递增区间,求a的取值范围.
(2)证明:当a>0时,函数在f(x)在区间(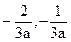 )上不存在零点
)上不存在零点
设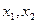 是函数
是函数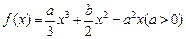 的两个极值点,且
的两个极值点,且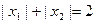
(Ⅰ)求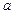 的取值范围;
的取值范围;
(Ⅱ)求证: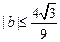 .
.