1990年3月,紫金山天文台将1965年9月20日发现的第2752号小行星命名为吴健雄星,其直径为32 km,如该小行星的密度和地球相同,已知地球半径R=6400km,地球的第一宇宙速度为8 km/s.求:该小行星第一宇宙速度?
如图甲所示,匀强磁场方向垂直纸面向里,磁场宽度为3L,正方形金属框边长为L,每边电阻均为R/4,金属框以速度υ的匀速直线穿过磁场区,其平面始终保持与磁感线方向垂直,当金属框 cd边到达磁场左边缘时,匀强磁场磁感应强度大小按如图乙所示的规律变化。
(1)求金属框进入磁场阶段,通过回路的电荷量;
(2)在图丙i—t坐标平面上画出金属框穿过磁场区的过程中,金属框内感应电流i随时间t的变化图线(取逆时针方向为电流正方向);
(3)求金属框穿过磁场区的过程中cd边克服安培力做的功W。
如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方放存在匀强磁场和匀强电场,磁场的磁感应强度为B,方向垂直xOy平面向里,电场线平行于y轴。一质量为m、电荷量为q的带电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴正方向夹角为θ,不计空气阻力,重力加速度为g,求:
(1)电场强度E的大小和方向;(2)小球从A点抛出时初速度v0的大小;(3)A点到x轴的高度h。
质量M=3kg的长木板放在水平光滑的平面上,在水平恒力F=11N作用下由静止开始向右运动,如图所示,当速度达到1m/s时,将质量m=4kg的物体轻轻放到木板的右端,已知物块与木板间摩擦因素μ=0.2,(g=10m/s2),求:
(1)物体经多长时间才与木板保持相对静止;
(2)物块与木板相对静止后,物块受到的摩擦力多大?
如图所示,在光滑的水平桌面上有一长为L=2 m的木板C,它的两端各有一块挡板,C的质量为mC=5 kg,在C的中央并排放着两个可视为质点的滑块A与B,其质量分别为mA=1 kg、mB=4 kg,开始时A、B、C均处于静止状态,并且A、B间夹有少许炸药,炸药爆炸使得A以vA=6 m/s的速度水平向左运动,不计一切摩擦,两滑块中任意一块与挡板碰撞后就与挡板合成一体,爆炸与碰撞时间不计,求: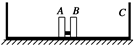
(1)当两滑块都与挡板碰撞后,板C的速度多大?
(2)从爆炸开始到两个滑块都与挡板碰撞为止,板C的位移多大?方向如何?
如图所示,A车的质量为m,沿光滑水平面以速度v1向质量为4m静止的B车运动,B车后面有弹簧,将弹簧压缩,设在整个过程中始终处于弹簧的弹性限度内,求在此运动过程中:
(1)弹簧的最大弹性势能;
(2)B车的最大速度。