阅读下列材料,并解决后面的问题.
★阅读材料:
我国是历史上较早发现并运用“勾股定理”的国家之一.我中古代把直角三角形中较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”,“勾股定理”因此而得名.
勾股定理:如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.请运用“勾股定理”解决以下问题: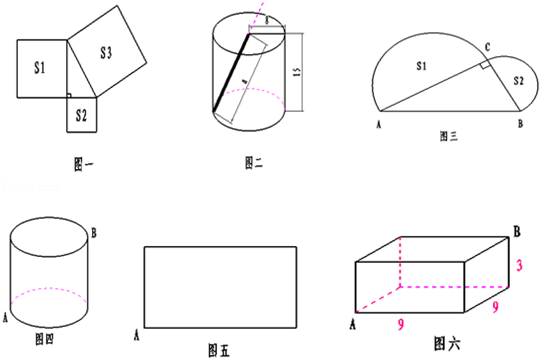
(1)如图一,分别以直角三角形的边为边长作正方形,其中s1=400,s2=225,则s3= .
(2)如图二,是一个园柱形饮料罐,底面半径=8,高=15,顶面正中有一个小园孔,则一条直达底部的直吸管的最大长度是 .注:罐壁厚度和顶部园孔直径忽略不计.
(3)如图三,所示的直角三角形中,AB=6.则s1+s2的值= . 注π值取3.
(4)如图四的圆柱,高=5厘米,底面半径=4厘米,在园柱底面A点有一只蚂蚁,它想吃到与A点相对的B点处的食物,需要爬行的路程是多少?小聪是这样思考的:
①将该园柱的侧面展开后得到一个长方形,如图五所示(A点的位置已经给出),请在图中中标出B点的位置并连接AB.
②小聪认为线段AB的长度是蚂蚁爬行的最短路程,那么蚂蚁爬行的最短路程是 厘米.注:π值取3.
(5)如图六,在长方形的底面A点有一只蚂蚁,想吃到上底面与A点相对的B点处的食物,它沿长方形表面爬行的最短路程是 厘米.
只列式,不计算.
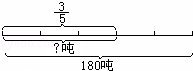
(1)列式 180×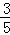 .
.
(2)从30里减去x的3倍,差是18,求x.列式
(3)6与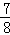 的和乘2与
的和乘2与 的差,积是多少?列式 (6+
的差,积是多少?列式 (6+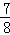 )×(2﹣
)×(2﹣ ) .
) .
用递等式计算.
(1)60﹣4.5×0.4
(2)3×(150﹣1530÷15)
(3)(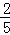 +
+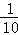 )×
)×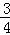 .
.
计算.(能简算的要简算)
560+1440÷12×5
3.5÷0.125×8
8×(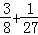 )+
)+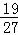
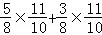 .
.
计算下面各题.
8470﹣104×65
7.12×4﹣1.12÷0.25
72× +10
+10
(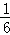 +
+ ﹣
﹣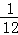 )×3
)×3
1﹣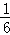 ÷
÷
1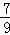 ×[(
×[( +0.25)÷(
+0.25)÷( ﹣
﹣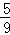 )].
)].
用递等式计算下面各题.
(1)4789﹣5768÷56×27
(2)(5.1÷0.17+4.2)×4.5
(3)(0.75﹣ )×(
)×( +
+ )
)
(4) ÷〔(
÷〔(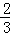 +
+ )×
)× 〕
〕