已知O是坐标原点，点A的坐标是（5，0），点B是y轴正半轴上一动点，以OB，OA为边作矩形OBCA，点E，H分别在边BC和边OA上，将△BOE沿着OE对折，使点B落在OC上的F点处，将△ACH沿着CH对折，使点A落在OC上的G点处。
（1）求证：四边形OECH是平行四边形；
（2）当点B运动到使得点F，G重合时，求点B的坐标，并判断四边形OECH是什么四边形？说明理由；
（3）当点B运动到使得点F，G将对角线OC三等分时，求点B的坐标。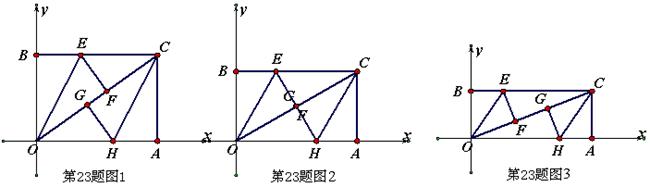
一根弹簧，原来的长度为8厘米，当弹簧受到拉力F时(F在一定范围内),弹簧的长度用L表示，测得有关数据如下表：
| 拉力F/千克 |
1 |
2 |
3 |
4 |
… |
| 弹簧的长度L/厘米 |
8+0.5 |
8+1.0 |
8+1.5 |
8+2.0 |
… |
（1）写出用拉力F表示弹簧的长度L的公式；
（2）若挂上8千克重的物体，则弹簧的长度是多少？
（3）需挂上多重的物体，弹簧长度为13厘米？
小虫从某点O出发在一直线上来回爬行，假定向右爬行的路程记为正数，向左爬行的路程记为负数，各段路程依次为（单位：cm）：+5，－3，+10，－8，－6，+12，－13.
（1）小虫最后在出发点O的哪个方向？相距多少厘米？
（2）小虫离出发点O最远是多少厘米？
（3） 在爬行过程中，如果每爬行1厘米奖励一粒芝麻，则小虫一共得到多少粒芝麻？
已知m、x、y满足：（1）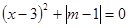
，（2）
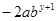与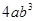
是同类项.求代数式：
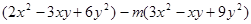的值.
如图AB∥DE，∠1=∠2，试说明AE∥DC．下面是解答过程，请你填空或填写理由．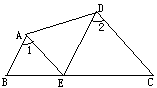
解：
AB∥DE（已知）
（ ）
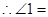又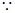∠1=∠2 （已知）
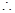∠2＝ （等量代换）
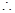AE∥DC．（ ）.
如图，这是一个由小立方体搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方体的个数，请你画出它的正视图与左视图.