演绎推理“因为对数函数 是增函数,而函数
是增函数,而函数 是对数函数,所以
是对数函数,所以 是增函数”所得结论错误的原因是( ).
是增函数”所得结论错误的原因是( ).
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.大前提和小前提都错误 |
一个几何体的三视图如图所示,正视图和侧视图都是等边三角形。若该几何体的四个顶点在空间直角坐标系 中的坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标可能为
中的坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标可能为
| A.(1,1,1) | B.(1,1, ) ) |
C.(1,1, ) ) |
D.(2,2, ) ) |
已知全集 ,
, ,
, ,则集合
,则集合 =
=
A. |
B. |
C. |
D. |
已知z为复数, (i为虚数单位),则
(i为虚数单位),则 =
=
A. |
B. |
C. |
D. |
已知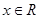 ,符号
,符号 表示不超过
表示不超过 的最大整数,若函数
的最大整数,若函数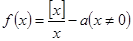 有且仅有3个零点,则
有且仅有3个零点,则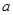 的取值范围是()
的取值范围是()
A.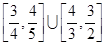 |
B.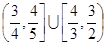 |
C.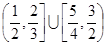 |
D. |
已知双曲线 右支上的一点
右支上的一点 到左焦点的距离与到右焦点的距离之差为
到左焦点的距离与到右焦点的距离之差为 ,且到两条渐进线的距离之积为
,且到两条渐进线的距离之积为 ,则该双曲线的离心率为()
,则该双曲线的离心率为()
A.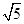 |
B.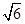 |
C.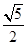 |
D.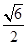 |