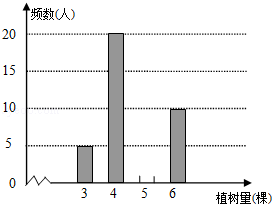
今年植树节,安庆某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
| 植树数量(棵) |
频数(人) |
频率 |
| 3 |
5 |
0.1 |
| 4 |
20 |
0.4 |
| 5 |
|
|
| 6 |
10 |
0.2 |
| 合计 |
50 |
1 |
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的众数和中位数,并从描述数据集中趋势的量中选择一个恰当的量来估计该校1200名学生的植树数量.