如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD2=CA•CB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA= ,求BE的长.
,求BE的长.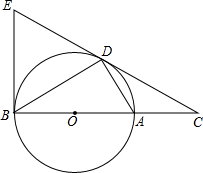
分解因式:15x(a-b)2-3y(b-a);
学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
| 一等奖 |
二等奖 |
三等奖 |
| 1盒福娃和1枚徽章 |
1盒福娃 |
1枚徽章 |
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和微章前,了解到如下信息: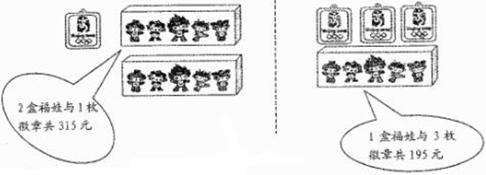
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?
某县响应“建设环保节约型社会”的号召,决定资助部分村镇修建一批沼气池,使农民用到经济、环保的沼气能源.幸福村共有264户村民,政府补助村里34万元,不足部分由村民集资.修建A型、B型沼气池共20个.两种型号沼气池每个修建费用、可供使用户数、修建用地情况如下表:
| 沼气池 |
修建费用(万元/个) |
可供使用户数(户/个) |
占地面积(m2/个) |
| A型 |
3 |
20 |
48 |
| B型 |
2 |
3 |
6 |
政府相关部门批给该村沼气池修建用地708平方米.设修建A型沼气池x个,修建两种型号沼气池共需费用y万元.
(1)用含有x的代数式表示y;
(2)不超过政府批给修建沼气池用地面积,又要使该村每户村民用上沼气的修建方案有几种;
(3)若平均每户村民集资700元,能否满足所需费用最少的修建方案.
某宾馆底层客房比二楼少5间,某旅行团有48人.若全部住底层,每间4人,房间不够;每间住5人,有房间没有住满5人.若全部安排在二楼,每间住3人,房间不够;每间住4人,有房间没有住满4人.问该宾馆底层有客房多少间?
某厂计划2004年生产一种新产品,下面是2003年底提供的信息,
人事部:明年生产工人不多于800人,每人每年可提供2400个工时;
市场部:预测明年该产品的销售量是10000~12000件;
技术部:该产品平均每件需要120个工时,每件要4个某种主要部件;
供应部:2003年低库存某种主要部件6000个.预测明年能采购到这种主要部件60000个.
根据上述信息,明年产品至多能生产多少件?