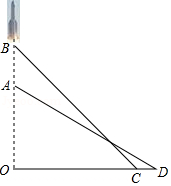
如图,已知抛物线y=2x2-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
(1)写出以A,B,C为顶点的三角形面积;
(2)过点E(0,6)且与x轴平行的直线l1与抛物线相交于M、N两点(点M在点N的左侧),以MN为一边,抛物线上的任一点P为另一顶点做平行四边形,当平行四边形的面积为8时,求出点P、N的坐标;
(3)过点D(m,0)(其中m>1)且与x轴垂直的直线l2上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长(用含m的代数式表示).
如图1,在等腰直角三角形 中, , .点 是 的中点,以 为边作正方形 ,连接 , .将正方形 绕点 顺时针旋转,旋转角为 .
(1)如图2,在旋转过程中,
①判断 与 是否全等,并说明理由;
②当 时, 与 交于点 ,求 的长.
(2)如图3,延长 交直线 于点 .
①求证: ;
②在旋转过程中,线段 的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.

为了探索函数 的图象与性质,我们参照学习函数的过程与方法.
列表:
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
描点:在平面直角坐标系中,以自变量 的取值为横坐标,以相应的函数值 为纵坐标,描出相应的点,如图1所示:
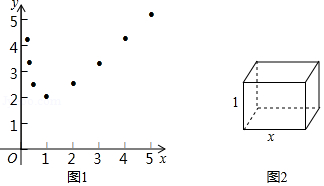
(1)如图1,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;
(2)已知点 , , , 在函数图象上,结合表格和函数图象,回答下列问题:
若 ,则 ;若 ,则 ;
若 ,则 (填" "," "或" " .
(3)某农户要建造一个图2所示的长方体形无盖水池,其底面积为1平方米,深为1米.已知底面造价为1千元 平方米,侧面造价为0.5千元 平方米.设水池底面一边的长为 米,水池总造价为 千元.
①请写出 与 的函数关系式;
②若该农户预算不超过3.5千元,则水池底面一边的长 应控制在什么范围内?
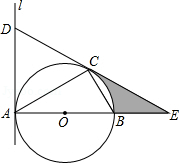
如图, 内接于 , 是 的直径.直线 与 相切于点 ,在 上取一点 使得 ,线段 , 的延长线交于点 .
(1)求证:直线 是 的切线;
(2)若 , ,求图中阴影部分的面积(结果保留 .
为支援抗疫前线,某省红十字会采购甲、乙两种抗疫物资共540吨,甲物资单价为3万元 吨,乙物资单价为2万元 吨,采购两种物资共花费1380万元.
(1)求甲、乙两种物资各采购了多少吨?
(2)现在计划安排 , 两种不同规格的卡车共50辆来运输这批物资.甲物资7吨和乙物资3吨可装满一辆 型卡车;甲物资5吨和乙物资7吨可装满一辆 型卡车.按此要求安排 , 两型卡车的数量,请问有哪几种运输方案?
2020年5月5日,为我国载人空间站工程研制的长征五号运载火箭在海南文昌首飞成功.运载火箭从地面 处发射,当火箭到达点 时,地面 处的雷达站测得 米,仰角为 .3秒后,火箭直线上升到达点 处,此时地面 处的雷达站测得 处的仰角为 .已知 , 两处相距460米,求火箭从 到 处的平均速度(结果精确到1米 秒,参考数据: , .