现场学习：在△ABC中，AB、BC、AC三边的长分别为
、
、
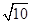，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．
（1）△ABC的面积为： _________ ；
（2）若△DEF三边的长分别为、
、
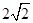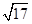，请在图1的正方形网格中画出相应的△DEF，并利用构图法求出它的面积；
（3）如图2，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13，10，17，且△PQR、△BCR、△DEQ、△AFP的面积相等，求六边形花坛ABCDEF的面积．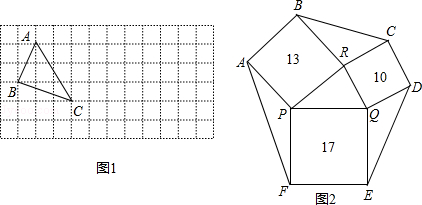
如图，在方格纸中，△ABC的三个顶点和点P都在小方格的顶点上，按要求画一个三角形，使它的顶点在方格的顶点上。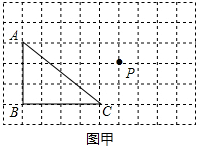
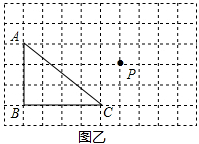
（1）将△ABC平移，使点P落在平移后的三角形内部，在图甲中画出示意图；
（2）以点C为旋转中心，将△ABC旋转，使点P落在旋转后的三角形内部，在图乙中画出示意图。
如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB，于点E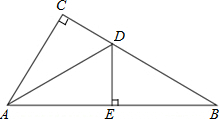
（1）求证：△ACD≌△AED；
（2）若∠B=30°，CD=1，求BD的长。
化简：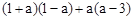
计算：
；
如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（6，0），B（0，8），点C的坐标为（0，m），过点C作CE⊥AB于点E，点D为x轴上一动点，连结CD，DE，以CD，DE为边作□CDEF。
（1）当0< m <8时，求CE的长（用含m的代数式表示）；
（2）当m =3时，是否存在点D，使□CDEF的顶点F恰好落在y轴上？若存在，求出点D的坐标；若不存在，请说明理由；
（3）点D在整个运动过程中，若存在唯一的位置，使得□CDEF为矩形，请求出所有满足条件的m的值。