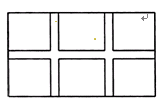
某商场销售甲、乙两种品牌的智能手机，这两种手机的进价和售价如下表所示：
| |
甲 |
乙 |
| 进价（元/部） |
4000 |
2500 |
| 售价（元/部） |
4300 |
3000 |
该商场计划购进两种手机若干部，共需15.5万元，预计全部销售后可获毛利润共2.1万元，［毛利润＝（售价－进价）×销售量］
（1）该商场计划购进甲、乙两种手机各多少部？
（2）通过商场调研，该商场决定在原计划的基础上，减少甲种手机的购进数量，增加乙种手机的购进数量，已知乙种手机增加数量是甲种手机减少的数量的2倍，而且用于购进这两种手机的总资金不超过16万元，该商场怎样进货，使全部销售后获得的毛利润最大？并求出最大毛利润。
使得函数值为零的自变量的值称为函数的零点。例如，对于函数
，令y=0，可得x=1，我们就说1是函数的零点。己知函数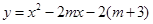
(
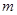m为常数)。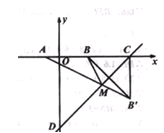
（1）当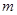=0时，求该函数的零点；
（2）证明：无论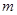取何值，该函数总有两个零点；
（3）设函数的两个零点分别为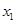
和
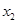，且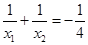
，此时函数图象与x轴的交点分别为A、B(点A在点B左侧)，点M在直线
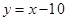上，当MA+MB最小时，求直线AM的函数解析式。
工艺商场按标价销售某种工艺品时，每件可获利45元；按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
（1）该工艺品每件的进价、标价分别是多少元？
（2）若每件工艺品按（1）中求得的进价进货，标价售出，工艺商场每天可售出该工艺品100件．若每件工艺品降价1元，则每天可多售出该工艺品4件．问每件工艺品降价多少元出售，每天获得的利润最大？获得的最大利润是多少？
关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2。
（1）求k的取值范围；
（2）如果x1+x2－x1x2＜－1且k为整数，求k的值。
如图，P是正三角形ABC 内的一点，且PA＝6，PB＝8，PC＝10。若将△PAC绕点A逆时针旋转后，得到△P/AB。⑴求点P与点P′之间的距离；⑵∠APB的度数。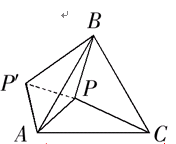
学校课外生物小组的试验园地是长20米，宽15米的长方形。为了便于管理，现要在中间开辟一横两纵等宽的小道（如图），要使种植面积为252平方米，求小道的宽。