某住宅区有12家住户,他们的门牌号分别是1,2,…,12.他们的电话号码依次是12个连续的六位自然数,并且每家的电话号码都能被这家的门牌号整除,已知这些电话号码的首位数字都小于6,并且门牌号是9的这一家的电话号码也能被13整除,问:这一家的电话号码是什么数?
认真做一做。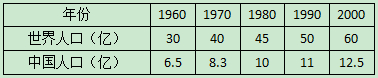
(1)这是从网上下栽的统计表。请将这些数据制成统计图。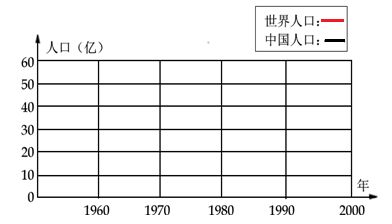
(2)从图上可以看出,近几十年来,中国人口和世界人口量都呈()趋势。
(3)中国人口数量在世界人口数量中所占的比例较(),到目前为止,基本上全世界()个人中就有一个中国人。
(4)看了这两组数据的对比,你有什么想法?
某电器店统计了去年空调和电暖器月销售情况,但是电暖器12月的销售量还没有整理出来。

(1)去年空调销售量最高的三个月分别是哪几个月?
(2)去年电暖器销售量最高的三个月有可能是哪几个月?
根据调查结果画出统计图并回答问题。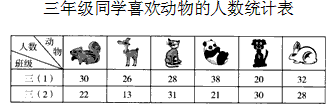
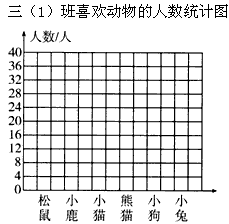
(1)这几种动物中,你最喜欢()。
(2)三(1)班喜欢()的人数多,三(2)班喜欢()的人数少。
(3)两个班喜欢熊猫的人数一共有()人。
下面是第26~29届奥运会上我国所获奖牌数量的统计表。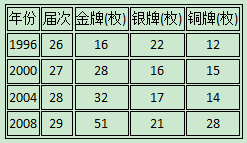
请根据上表画出我国在第26~ 29届奥运会上获金牌和银牌数量的折线统计图。
统计下面是某星期科技馆参观人数统计表。
(1)根据上表完成折线统计图。
(2)这组数据的平均数是(),中位数是()。
(3)星期六参观的人数比星期五增长了百分之几?(列式计算)