神奇的“莫比乌斯圈”
数学史上曾流传着这样一道趣题:用一张宽3cm、长30cm的白纸条,首尾粘连做成一个纸圈,然后在这个纸圈上涂颜色.只允许使用一种颜色,在纸圈的一个面涂抹,最后把整个纸圈全部涂成一种颜色,不留下一点空白.
对于这样一个看似简单的问题,几百年来,曾有许多科学家进行认真研究.德国著名的数学家莫比乌斯就经过长时间思考、实验,终于受田野里玉米叶子的启发,想出了解决方法:把纸条儿的一端扭转180゜,再将两端粘在一起,做成只有一个面、一条封闭曲线作边界的纸圈.
纸圈做成后,莫比乌斯提了一只小甲虫,放在上面让它爬.结果,小甲虫不翻越任何边界而爬遍了圆圈的所有部分.莫比乌斯激动地说:“公正的小甲虫,你无可辩驳地证明这个纸圈只有一个面.”
这个极其简单而又奇妙的纸圈,震动了整个科学界.后来,人们把它叫作“莫比乌斯圈”.
如图是张、王、李三个养鸡专业户产量统计图,如果他们三人共养鸡400万只,请算出:
(1)张养鸡 万只
(2)王养鸡 万只
(3)李养鸡 万只.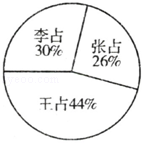
六年级二班的学生对本年级同学最喜欢的电视节目进行了调查,并绘制了扇形统计图.
(1)你能判断出喜欢哪种电视节目的人数最少吗?
(2)你有什么修改建议?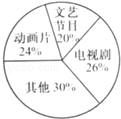
六年级某班上学期期未数学考试的成绩情况如图.
(1)从图中你能得到哪些信息?
(2)这个班得优秀的共有12人,得良好、及格和不及格的各有多少人?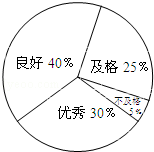
学校图书室文艺书、科技书、故事书的统计情况如右图.
(1)故事书有2500册,图书室共有这三类书多少册?
(2)科技书和文艺书分别有多少册?
(3)科技书比文艺书多百分之几?
在向贫困地区学校的捐书活动中.向阳小学各年级捐书情况如图:
(1)全校各年级共捐书2500册,3、4年级各捐了多少册?
(2)6年级比5年级多捐多少册?
(3)从上图中你能看出各年级捐书的规律吗?