如图，直线y=4x+4与x轴、y轴相交于B、C两点，抛物线y=ax2-2ax+c（a≠0）过点B、C，且与x轴另一个交点为A，以OC、OA为边作矩形OADC，CD交抛物线于点G．
（1）求抛物线的解析式以及点A的坐标；
（2）已知直线x=m交OA于点E，交CD于点F，交AC于点M，交抛物线（CD上方部分）于点P，请用含m的代数式表示PM的长；
（3）在（2）的条件下，联结PC，若△PCF和△AEM相似，求m的值．
如图，A（-1，0），C（1，4），点B在x轴上，且AB=3．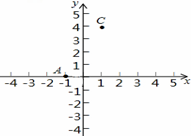
（1）求点B的坐标；
（2）求△ABC的面积；
（3）在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为10，若存在，请直接写出点P的坐标；若不存在，请说明理由．
一群驴友自助登山，登山前组织者给每人都发了矿泉水：若每人发2瓶，则剩余5瓶，若每人发4瓶，则其中有一人有矿泉水但不足4瓶．请求出驴友人数和矿泉水瓶数．
如图，已知△ABC、△ADE均为等边三角形，点D是BC延长线上一点，连结CE，求证：BD=CE
在平面直角坐标系中，已知△OAB，A(0，-3)，B(-2，0)．
（1）在图1中画出△OAB关于x轴的轴对称图形；
（2）将
先向右平移3个单位，再向上平移2个单位，在图2中画出平移后的图形；
（3）点A平移后的坐标为.
解不等式组：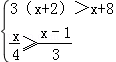
并把它的解集在数轴上表示出来．