如果执行右面的程序框图,那么输出的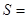 ( )
( )
| A.22 | B.46 | C.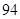 |
D.190 |
有不同的语文书9本,不同的数学书7本,不同的英语书5本,从中选出不属于同一学科的书2本,则不同的选法有( )种
| A.21 | B.315 | C.143 | D.153 |
某校高中生共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样抽取一个容量为45的样本,那么高一、高二、高三各年级抽取人数分别为( )
| A.15,5,25 | B.15,15,15 |
| C.10,5,30 | D.15,10,20 |
命题“存在 R,
R,
 0”的否定是( ).
0”的否定是( ).
A.不存在 R, R,  >0 >0 |
B.存在 R, R,   0 0 |
C.对任意的 R, R,   0 0 |
D.对任意的 R, R,  >0 >0 |
若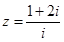 ,则复数
,则复数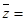 ( )
( )
A.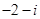 |
B. |
C.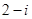 |
D. |