用数学归纳法证明1+2+3+…+n2= ,则当n=k+1时左端应在n=k的基础上加上( ).
,则当n=k+1时左端应在n=k的基础上加上( ).
| A.k2+1 |
| B.(k+1)2 |
C.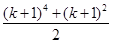 |
| D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2 |
设函数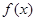 、
、 的定义域分别为F、G,且
的定义域分别为F、G,且 。若对任意的
。若对任意的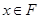 ,都有
,都有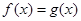 ,则称
,则称 为
为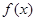 在G上的一个“延拓函数”。已知
在G上的一个“延拓函数”。已知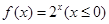 ,若
,若 为
为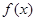 在R上的一个延拓函数,且
在R上的一个延拓函数,且 是偶函数,则
是偶函数,则 的解析式是()
的解析式是()
A. |
B.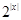 |
C. |
D.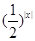 |
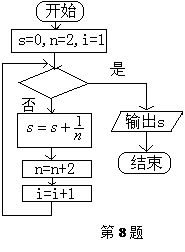
右图给出的是计算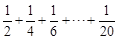 的值的一个程序框图,其中判断框内应填入的条件是( )
的值的一个程序框图,其中判断框内应填入的条件是( )
| A.i>10 | B.i<10 |
| C.i>20 | D.i>20 |
根据三角恒等变换,可得如下等式: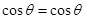 ;
;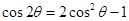 ;
;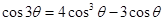 ;
;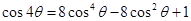 ;
;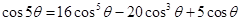 ;
;
依此规律,猜测 ,其中
,其中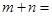 ()
()
A.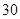 |
B.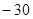 |
C. |
D.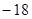 |
定义 ,将函数
,将函数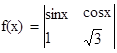 的图象向左平移
的图象向左平移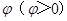 个单位长度后,得到函数g(x),若g(x)为奇函数,则
个单位长度后,得到函数g(x),若g(x)为奇函数,则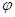 的值可以是( )
的值可以是( )
A.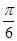 |
B.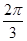 |
C.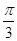 |
D.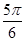 |
由直线x=-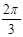 ,x=
,x=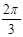 ,y=0与曲线y=cosx所围成的封闭图形的面积为()
,y=0与曲线y=cosx所围成的封闭图形的面积为()
A.2-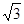 |
B.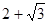 |
C.4-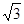 |
D. |