甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以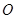 为起点,再从
为起点,再从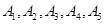 ,这
,这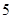 个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为 ,若
,若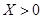 就让甲去;若
就让甲去;若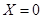 就让乙去;若
就让乙去;若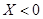 就是丙去.
就是丙去.
(Ⅰ)写出数量积 的所有可能取值;
的所有可能取值;
(Ⅱ)求甲、乙、丙三人去参加比赛的概率,并由求出的概率来说明这个规则公平吗?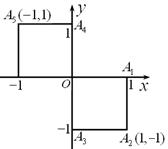
已知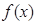 是定义在
是定义在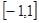 上的奇函数,且
上的奇函数,且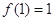 ,若
,若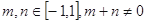 时,有
时,有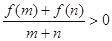
(1)证明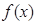 在
在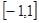 上是增函数;
上是增函数;
(2)解不等式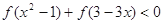
(3)若 对
对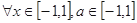 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
设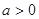 且
且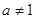 ,函数
,函数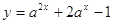 在
在 的最大值是14,求
的最大值是14,求 的值。
的值。
已知函数 是
是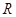 上的增函数,
上的增函数,
(1)若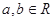 ,且
,且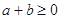 ,求证
,求证
(2)判断(1)中命题的逆命题是否成立,并证明你的结论。
已知定义在 上的奇函数
上的奇函数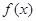 ,当
,当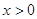 时,
时,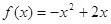
(1)求函数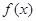 在
在 上的解析式;(2)若函数
上的解析式;(2)若函数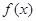 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下
| 男 |
女 |
合计 |
|
| 需要 |
40 |
30 |
|
| 不需要 |
160 |
270 |
|
| 合计 |
(1)将表格填写完整,并估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关系?
(3)根据(2)的结论,能否提出更好的调查方法估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附表:
| P(K2≥k) |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |