甲、乙两恒星相距为L，质量之比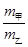
＝
，它们离其他天体都很遥远，我们观察到它们的距离始终保持不变，由此可知 （ ）．
| A．两恒星一定绕它们连线的某一位置做匀速圆周运动 |
| B．甲、乙两恒星的角速度之比为2∶3 |
C．甲、乙两恒星的线速度之比为 ∶ |
| D．甲、乙两恒星的向心加速度之比为3∶2 |
17世纪，意大利物理学家伽利略根据“斜面实验”指出：在水平面上运动的物体之所以会停下来，是因为受到摩擦阻力的缘故，你认为下列陈述正确的是
| A．该实验是一理想实验，是在思维中进行的，无真实的实验基础，故其结果是荒谬的。 |
| B．该实验是以可靠的事实为基础，经过抽象思维，抓住主要因素，忽略次要因素，从而更深刻地反映自然规律 |
| C．该实验证实了亚里士多德“力是维持物体运动的原因”的结论 |
| D．该实验为牛顿第一定律的提出提供了有力的实验依据 |
探究力的平行四边形定则的实验原理是等效原理，其等效性是指
| A．使两分力与合力满足平行四边形定则 |
| B．使两次橡皮筋与细绳套的结点都与某点O重合 |
| C．使两次橡皮筋伸长的长度相等 |
| D．使弹簧测力计在两种情况下发生相同的形变 |
如图所示，用与竖直方向成
角的倾斜轻绳
和水平轻绳b共同固定一个小球，这时绳b的拉力为
。现在保持小球在原位置不动，使轻绳b在原竖直平面内逆时针转过角固定，轻绳b拉力变为
；再逆时针转过角固定，绳b拉力变为
，则
A． |
B． |
C． |
D． |
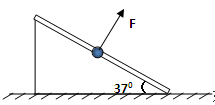
如图所示，重为10N的小球套在与水平面成370角的硬杆上，现用一垂直于杆向上、大小为20N的力F拉小球，使小球处于静止状态（已知
）
| A．小球不一定受摩擦力的作用 |
| B．小球受摩擦力的方向一定沿杆向上，大小为6N |
| C．杆对小球的弹力方向垂直于杆向下，大小为4.8N |
| D．杆对小球的弹力方向垂直于杆向上，大小为12N |
一质点运动的位移一时间图像如图所示，则关于质点的运动，下列说法正确的是
| A．0-1s内质点的运动方向与加速度方向相同 |
| B．1-2s内质点的速度大小增加 |
| C．2-3s内质点的运动方向为负方向 |
| D．4s时刻质点的速度最大 |