如图,把一个质量为m的小球用细线悬挂起来,就成为一个摆,细线长为L(小球的半径忽略),最大偏角为θ,忽略空气阻力,重力加速度为g,求小球运动到最低点O时细线对小球的拉力。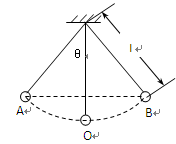
如图所示(1),在粗糙的水平地面上,放有一块质量为m="1" kg,初速度为v0的木块,现在加水平恒力F,方向与初速度的方向在同一条直线上,通过实验发现不同的F,物块在地面运动的时间t不同,且当-2 N≤F<2 N时,1/t与F的关系如图(2)所示(设v0的方向为正、滑动摩擦力等于最大静摩擦力),则
(1)物块的初速度为多少?
(2)物块与地面间的动摩擦因素为多少?
(3)物块运动的时间t可能等于0.4 s吗?说明原因.
如图甲所示,水平传送带的长度L=6 m,皮带轮的半径R=0.25 m,皮带轮以角速度ω顺时针匀速转动.现有一质量为1 kg的小物体(视为质点)以水平速度v0从A点滑上传送带,越过B点后做平抛运动,其水平位移为x.保持物体的初速度v0不变,多次改变皮带轮的角速度ω,依次测量水平位移x,得到如图乙所示的x-ω图象.已知重力加速度g=10 m/s2.回答下列问题: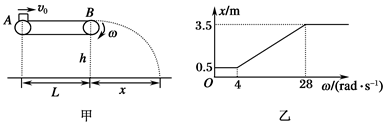
(1)当0<ω<4 rad/s时,物体在A、B之间做什么运动?
(2)物块的初速度v0为多大?
(3)B端距地面的高度h为多大?
(4)当ω=24 rad/s时,求传送带对物体做的功.
某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=60kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=5.0m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内,若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8, g=10m/s2)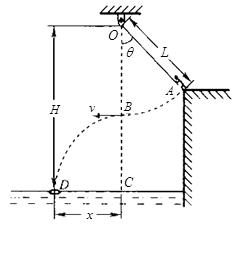
(1)求参赛者经过B点时速度的大小v;
(2)求参赛者从台阶上A点跃出时的动能EK;
(3)若手与绳之间的动摩擦因数为0.6,参赛者要顺利完成比赛,则每只手对绳的最大握力不得小于多少?(设最大静摩擦等于滑动摩擦力)
有一辆可自动变速的汽车,总质量为1000 kg,行驶中,该车速度在14 m/s至20 m/s范围内可保持恒定功率20 kW不变.一位同学坐在驾驶员旁观察车内里程表和速度表,记录了该车在位移120 m至400 m范围内做直线运动时的一组数据如下:
| l/m |
120 |
160 |
200 |
240 |
280 |
320 |
360 |
400 |
| v/m·s-1 |
14.5 |
16.5 |
18.0 |
19.0 |
19.7 |
20.0 |
20.0 |
20.0 |
根据上面的数据回答下列问题.(设汽车在上述范围内受到的阻力大小不变)
(1)估算该汽车受到的阻力为多大?
(2)在位移120 m至320 m过程中牵引力所做的功约为多大?
(3)在位移120 m至320 m过程中所花的时间是多少?
如图,质量m=2kg的物体静止于水平地面的A处,A、B间距L=20m.用大小为30N,沿水平方向的外力拉此物体,经t0=2s拉至B处.
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为20N的力,沿水平方向拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t.(取g=10 m/s2)