方程ax2＋2x＋1＝0至少有一个负实根的充要条件是（ ）
| A．0<a≤1 | B．a<1 | C．a≤1 | D．0<a≤1或a<0 |
已知集合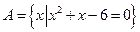
，
，若
，则实数
的取值集合
是
A． |
B． |
C． |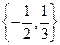
D． |
集合
，
。若
，则
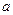的值为
| A．0 | B．1 | C．2 | D．4 |
若
的周长等于
，面积是
，
，则
边的长是
A、5 B、6 C、7 D
、8
若对可导函数f(x)，g(x)，当x∈[0,1]时，恒有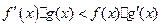
，已知α、β是一个锐角三角形
的两个内角，且α≠β，记F（x）=
(g(x) ≠0)，则下列不等式正确的是（ ）
| A．F（sinα）<F(sinβ) | B．F（cosα）> F（sinβ） |
C．F(cosα)> F(c osβ) |
D．F(cosα)< F(cosβ) |
若f(x)=－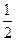
x2+bln(x+2)在（－1，+∞）上为减函数，则b的取值范围是（ ）
| A．[－1，+∞） | B．（－1，+∞） | C．（－∞，－1） | D．（－∞，－1] |