数学课上,张老师出示了问题:如图1,△ABC是等边三角形,点D是边BC的中点.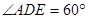 ,且DE交△ABC外角
,且DE交△ABC外角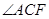 的平分线CE于点E,求证:AD=DE.
的平分线CE于点E,求证:AD=DE.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接MD,则△BMD是等边三角形,易证△AMD≌△DCE,所以AD=DE.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点D是边BC的中点”改为“点D是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AD=DE”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小亮提出:如图3,点D是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AD=DE”仍然成立.你认为小华的观点 (填“正确”或“不正确”).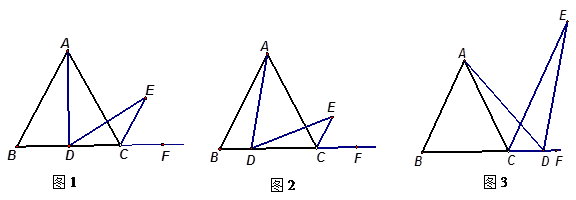
解分式方程: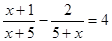 .
.
先化简,再求值: ,其中
,其中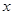 =3.
=3.
因式分解:
(1)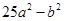 ;(2)
;(2)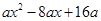 .
.
(12分)八年级(1)班准备组织学生出去旅游,班长选择了一家旅行社去咨询费用,该家旅行社承诺组团旅行人数在50人以上(不包括50人),可享受优惠价,但组团人数在50人以下(包括50人),只能按原价付费。班长计算了一下,若按现在班级人数购票,只能按原价付费,需用900元;于是班长邀请了10位家长参与这次活动,那么就可以享受优惠价,只需880元.请解答下列问题:
(1)八年级(1)班的学生人数在什么范围内?
(2)若按优惠价10人的旅游费用与按原价8人的旅游费用相同,那么八年级(1)班共有多少名学生?
(12分)用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
| 原料 维生素及价格 |
甲种原料 |
乙种原料 |
| 维生素C/(单位/千克) |
600 |
100 |
| 原料价格/(元/千克) |
8 |
4 |
现配制这种饮料10千克,,要求至少含有4000单位的维生素C,并且购买甲、乙两种原料的费用不超过72元,若购买甲种原料的质量为x(整数)千克,请解答下列问题:
(1)购买甲、乙两种原料有哪几种方案?
(2)哪种购买方案的费用最低?最低费用是多少元?