设椭圆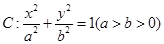 的左、右焦点分别为
的左、右焦点分别为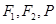 是
是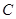 上的点
上的点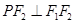 ,
,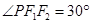 ,则椭圆
,则椭圆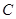 的离心率为()
的离心率为()
A.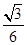 |
B. |
C.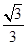 |
D.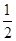 |
若函数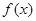 和
和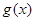 的定义域、值域都是
的定义域、值域都是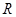 ,则不等式
,则不等式 有解的充要条件是()
有解的充要条件是()
A. |
B.有无穷多个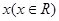 ,使得 ,使得 |
C.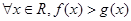 |
D.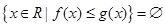 |
观测两个相关变量,得到如下数据:
 |
 |
 |
 |
 |
 |
5 |
4 |
3 |
2 |
1 |
 |
 |
 |
 |
 |
 |
5 |
4.1 |
2.9 |
2.1 |
0.9 |
则两变量之间的线性回归方程为()
A. B.
B. C.
C. D.
D.
 中,
中, ,
, ,则
,则 ()
()
A. |
B. |
C. |
D. |
下面是一段演绎推理:
如果直线平行于平面,则这条直线平行于平面内的所有直线;
已知直线 平面
平面 ,直线
,直线 平面
平面 ;
;
所以直线 直线
直线 ,在这个推理中()
,在这个推理中()
| A.大前提正确,结论错误 |
| B.小前提与结论都是错误的 |
| C.大、小前提正确,只有结论错误 |
| D.大前提错误,结论错误 |