已知 .
.
(Ⅰ)求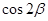 的值;
的值;
(Ⅱ)求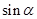 的值.
的值.
设函数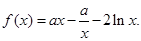
(Ⅰ)若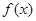 在
在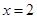 时有极值,求实数
时有极值,求实数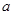 的值和
的值和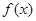 的单调区间;
的单调区间;
(Ⅱ)若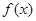 在定义域上是增函数,求实数
在定义域上是增函数,求实数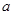 的取值范围.
的取值范围.
已知函数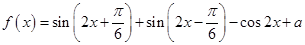 (
(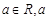 为常数).
为常数).
(1)求函数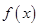 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)若函数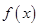 的图像向左平移
的图像向左平移 个单位后,得到函数
个单位后,得到函数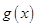 的图像关于
的图像关于 轴对称,求实数
轴对称,求实数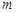 的最小值.
的最小值.
甲乙丙三人商量周末去玩,甲提议去市中心逛街,乙提议去城郊觅秋,丙表示随意。最终,商定以抛硬币的方式决定结果。规则是:由丙抛掷硬币若干次,若正面朝上则甲得一分乙得零分,反面朝上则乙得一分甲得零分,先得4分者获胜,三人均执行胜者的提议.记所需抛币次数为 .
.
⑴求 =6的概率;
=6的概率;
⑵求 的分布列和期望.
的分布列和期望.
已知函数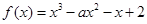 (
(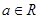 ).
).
(Ⅰ)当 时,求函数
时,求函数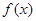 的极值;
的极值;
(Ⅱ)若对任意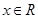 ,不等式
,不等式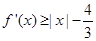 恒成立,求实数
恒成立,求实数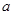 的取值范围.
的取值范围.
已知椭圆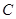 :
: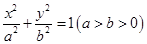 的离心率为
的离心率为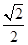 ,左焦点为
,左焦点为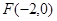 .
.
(Ⅰ)求椭圆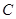 的方程;
的方程;
(Ⅱ)若直线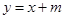 与曲线
与曲线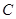 交于不同的
交于不同的 、
、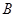 两点,且线段
两点,且线段 的中点
的中点 在圆
在圆 上,求
上,求 的值.
的值.