已知点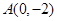
，椭圆
：
的离心率为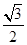
，
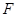是椭圆的焦点，直线
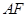的斜率为
，
为坐标原点.
（1）求的方程；
（2）设过点
的直线
与相交于
两点，当
的面积最大时，求
的方程.
某工厂生产某种产品,每日的成本C(单位:元)与日产量x(单位:吨)满足函数关系式C=10000+20x,每日的销售额R(单位:元)与日产量x满足函数关系式R=
已知每日的利润y=R-C,且当x=30时,y=-100.
(1)求a的值.
(2)求当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.
已知函数f(x)=x3-3x.
(1)求函数f(x)的单调区间.
(2)求函数f(x)在区间[-3,2]上的最值.
已知两函数f(x)=8x2+16x-k,g(x)=2x3+5x2+4x,其中k为实数.
(1)对任意x∈[-3,3]都有f(x)≤g(x)成立,求k的取值范围.
(2)存在x∈[-3,3]使f(x)≤g(x)成立,求k的取值范围.
(3)对任意x1,x2∈[-3,3]都有f(x1)≤g(x2),求k的取值范围.
设f(x)=-
x3+
x2+2ax.
(1)若f(x)在(
,+∞)上存在单调递增区间,求a的取值范围.
(2)当0<a<2时,f(x)在[1,4]上的最小值为-
,求f(x)在该区间上的最大值.
已知函数f(x)=lnx+ax+1,a∈R.
(1)求f(x)在x=1处的切线方程.
(2)若不等式f(x)≤0恒成立,求a的取值范围.