如图，对称轴为直线x=2的抛物线经过点A（-1，0），C（0，5）两点，与x轴另一交点为B，已知M（0，1），E（a，0），F（a+1，0），点P是第一象限内的抛物线上的动点．
（1）求此抛物线的解析式；
（2）当a=1时，求四边形MEFP面积的最大值，并求此时点P的坐标；
（3）若△PCM是以点P为顶点的等腰三角形，求a为何值时，四边形PMEF周长最小？请说明理由．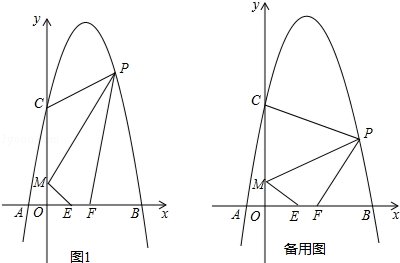
（1）先化简，再求值：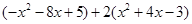
，其中
．
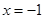（2）两个多项式的和是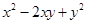
，其中一个多项式是
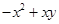，求另一个多项式．
计算：（1）
（2）
计算：（1）
（2）
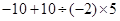
（3）
画出数轴，在数轴上表示下列各数：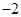
，1.5，0，
，4，并回答问题：
（1）按从小到大的顺序用“＜”连接上面各数；
（2）在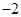，1.5，0，，4这五个数中，任取二个数相乘，其中最大的积是 *．
我们知道，平方差公式是： (a+b)(a-b) = a2 - b2，反过来得到：a2 - b2=(a+b)(a-b)也成立，在解决某些问题时逆用平方差公式会起到很好的效果，如：计算：
根据平方差逆用方法，请计算下列各题：
(1) 
；(2分)
(2) 正整数m、n满足m2- n2=7，求m、n的值.(3分)