已知双曲线y=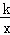 (k>0),过点M(m,m)(m>
(k>0),过点M(m,m)(m>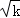 )作MA⊥x轴,MB⊥y轴,垂足分别是A和B,MA、MB分别交双曲线y=
)作MA⊥x轴,MB⊥y轴,垂足分别是A和B,MA、MB分别交双曲线y=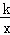 (k>0)于点E、F。
(k>0)于点E、F。
(1)若k=2,m=3,求直线EF的解析式;
(2)O为坐标原点,连接OF,若∠BOF=22.5°,多边形BOAEF的面积是2,求k值。
画图:牧童在A处放牛,其家在B处,若牧童从A处将牛牵到河边C处饮水后再回家,试问C在何处,所走路程最短?(保留作图痕迹)
某地电话拨号上网有两种收费方式,用户可以任选一种。
A、计时制,每分钟0.05元;
B、包月制:每月50元(限一部个人住宅电话上网)。
此外,每种上网方式都要增收每分钟0.02元的通讯费
(1)某用户某月上网时间为x小时,请用代数式表示两种收费方式下,该用户分别应支付的费用。
A:B:
(2)若某用户估计每月上网时间为20小时,通过计算说明应该采用哪一种付费方式较为合算。
若“△”表示一种新运算,规定a△b=a×b-(a+b),请计算下列各式的值
(1)-3△5(2)2△[(-4)△(-5)]
如图,正方形的边长为a,用整式表示图中阴影部分的面积,并计算当a=2时阴影部分的面积( 取3.14)
取3.14)
已知a、b两数在数轴上表示如图
(1)试在数轴上找出表示-a,-b的点,并用“<”连接a,b,-a,-b
(2)化简:|a-b|-|b|+|a|