在竖直的井底，将一物块以11 m/s的速度竖直地向上抛出，物块冲过井口再落回到井口时被人接住，在被人接住前1 s内物块的位移是4 m，位移方向向上，不计空气阻力，g取10 m/s2，求：
（1）物块从抛出到被人接住所经历的时间；
（2）此竖直井的深度．
宇航员站在某一星球表面上的某高度，沿水平方向抛出一小球，经过时间t，小球落到星球表面上，测得抛出点与落地点之间的距离为
.若抛出时的初速度增大到2倍，则抛出点与落地点之间的距离为
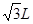.已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G.不计空气阻力，求该星球的质量
．
已知某星球的半径为R，星球的质量为
,它的自转周期为T,有一质量为
的物体静置于该星球的赤道上，试求物体所受的支持力ＦＮ有多大？（不能忽略星球的自转）
如图所示，一个人用一根长为R=1米，能承受最大拉力为F=74N的绳子，系着一个质量为m=1Kg的小球，在竖直平面内作圆周运动，已知圆心O离地面高h=6米。运动中小球在圆周的最低点时绳子刚好被拉断，绳子的质量和空气阻力均忽略不计，g="10" m/s2．求：
（1）绳子被拉断的瞬间，小球的速度v的大小？
（2）绳断后，小球落地点与圆周的最低点间的水平距离x多大？
如图所示，长度为
的轻绳，一端栓着一质量
的小球在竖直面内做圆周运动，小球可视为质点，已知绳子能够承受的最大拉力为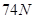
，圆心离地面高度为
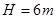，小球在运动过程中绳子始终处于绷紧状态。求：
（1）分析绳子在何处最易断，求出绳子断裂时小球的线速度大小；
（2）绳子断裂后小球做平抛运动的时间及落地点与抛出点的水平距离。
2003年10月15日，我国神舟五号载人飞船成功发射。飞船在绕地球飞行5圈后进行变轨，由原来的椭圆轨道变为距地面高度为h的圆形轨道，已知地球半径为R，地面处的重力加速度为g。求：
(1)飞船在上述圆形轨道上运行的速度v；
(2)飞船在上述圆形轨道上运行的周期T。