如图所示,内圆半径为r、外圆半径为3r的圆环区域内有垂直纸面向里、磁感应强度为B的匀强磁场。圆环左侧的平行板电容器两板间电压为U,靠近M板处静止释放质量为m、 电量为q的正离子,经过电场加速后从N板小孔射出,并沿圆环直径方向射入磁场,不计离子的重力,忽略平行板外的电场。求:
(1)离子从N板小孔射出时的速率;
(2)离子在磁场中做圆周运动的周期;
(3)要使离子不进入小圆区域,电压U的取值范围。
如图所示,电阻不计足够长的光滑平行金属导轨与水平面夹角 ,导轨间距
,导轨间距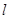 ,所在平面的正方形区域
,所在平面的正方形区域 内存在有界匀强磁场,磁感应强度为
内存在有界匀强磁场,磁感应强度为 T,方向垂直斜面向上.甲、乙金属杆质量均为
T,方向垂直斜面向上.甲、乙金属杆质量均为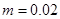 kg、电阻相同,甲金属杆处在磁场的上边界,乙金属杆距甲也为
kg、电阻相同,甲金属杆处在磁场的上边界,乙金属杆距甲也为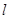 ,其中
,其中 m.同时无初速释放两金属杆,此刻在甲金属杆上施加一个沿着导轨的外力
m.同时无初速释放两金属杆,此刻在甲金属杆上施加一个沿着导轨的外力 ,保持甲金属杆在运动过程中始终与乙金属杆未进入磁场时的加速度相同.且乙金属杆进入磁场后恰能做匀速直线运动,(取
,保持甲金属杆在运动过程中始终与乙金属杆未进入磁场时的加速度相同.且乙金属杆进入磁场后恰能做匀速直线运动,(取 m/s2)
m/s2)
(1)计算乙的电阻 .
.
(2)以刚释放两杆时作为零时刻,写出从开始到甲金属杆离开磁场的过程中,外力 随时间
随时间 的变化关系,并说明
的变化关系,并说明 的方向.
的方向.
(3)若从开始释放到乙金属杆离开磁场,乙金属杆中共产生热量 J,试求此过程中外力
J,试求此过程中外力 对甲做的功.
对甲做的功.
如图所示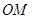 、
、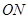 相互垂直,
相互垂直, 将空间分成两个区域,
将空间分成两个区域, .区域Ⅰ中有垂直于纸面向外的匀强磁场,区域Ⅱ中有平行于
.区域Ⅰ中有垂直于纸面向外的匀强磁场,区域Ⅱ中有平行于 ,大小为
,大小为 的匀强电场和另一未知匀强磁场(方向垂直纸面,图中未画出).一束质量为
的匀强电场和另一未知匀强磁场(方向垂直纸面,图中未画出).一束质量为 、电量为
、电量为 的粒子以不同的速率(速率范围0~
的粒子以不同的速率(速率范围0~ )自
)自 点垂直于
点垂直于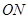 射入区域Ⅰ.其中以最大速率
射入区域Ⅰ.其中以最大速率 射入的粒子恰能垂直于
射入的粒子恰能垂直于 进入区域Ⅱ.已知
进入区域Ⅱ.已知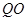 间距为
间距为 ,不计粒子重力以及粒子间的相互作用.试求:
,不计粒子重力以及粒子间的相互作用.试求:
(1)区域Ⅰ中匀强磁场的磁感应强度大小;
(2)为使速率为 的粒子进入区域Ⅱ后能沿直线运动,则区域Ⅱ的磁场大小和方向;
的粒子进入区域Ⅱ后能沿直线运动,则区域Ⅱ的磁场大小和方向;
(3)分界线 上,有粒子通过的区域的长度.
上,有粒子通过的区域的长度.
如图甲所示,一个电阻值为 ,匝数为
,匝数为 的圆形金属线圈与
的圆形金属线圈与
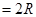 的电阻连结成闭合回路.线圈的半径为
的电阻连结成闭合回路.线圈的半径为 .在线圈中半径为
.在线圈中半径为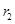 的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度
的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度 随时间
随时间 变化的关系图线如图乙所示.图线与横、纵轴的截距分别为
变化的关系图线如图乙所示.图线与横、纵轴的截距分别为 和
和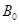 .导线的电阻不计.求0至
.导线的电阻不计.求0至 时间内:
时间内:
(1)通过电阻 上的电流大小和方向;(2)通过电阻
上的电流大小和方向;(2)通过电阻 上的电量
上的电量 及电阻
及电阻 上产生的热量.
上产生的热量.
如图所示,某种自动洗衣机进水时,洗衣机缸内水位升高,与洗衣缸相连的细管中会封闭一定质量的空气(可视为理想气体),通过压力传感器可感知管中的空气压力,从而控制进水量.若进水前细管内空气的体积为 ,压强为
,压强为 ,当洗衣缸内水位缓慢升高(假设细管内空气温度不变),被封闭空气的压强变为
,当洗衣缸内水位缓慢升高(假设细管内空气温度不变),被封闭空气的压强变为 时(
时( >1).求:细管内进水的体积.
>1).求:细管内进水的体积.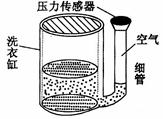
如图所示,BCDG是光滑绝缘的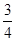 圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为
圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为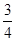 mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.
mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.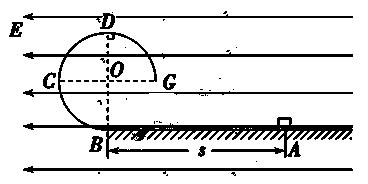
(1)若滑块从水平轨道上距离B点s=3R的A点由静止释放,滑块到达与圆心O等高的C点时速度为多大?
(2)在(1)的情况下,求滑块到达C点时受到轨道的作用力大小;
(3)改变s的大小,使滑块恰好始终沿轨道滑行,且从G点飞出轨道,求滑块在圆轨道上滑行过程中的最小速度大小.