脱式计算.
15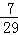 ﹣(5
﹣(5 +3
+3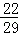 )﹣4
)﹣4 1
1 ×43×70%﹣2÷
×43×70%﹣2÷
[2.1+7÷(3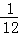 ﹣1
﹣1 )]×1
)]×1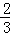 (
( ×5÷
×5÷ ×5)×(1.685÷1
×5)×(1.685÷1 ﹣0.235×
﹣0.235× )
)
1﹣[4 ﹣(31%﹣
﹣(31%﹣ )×16
)×16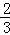 ]÷1
]÷1 15
15 ÷63%﹣[24
÷63%﹣[24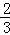 ﹣8
﹣8 ×(3
×(3 ﹣287.5%)]
﹣287.5%)]
直接写出得数: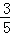 ÷60%= 7﹣3.2﹣2.8=(0.75﹣
÷60%= 7﹣3.2﹣2.8=(0.75﹣ )×16=
)×16=
6.76+3.24= ﹣
﹣ =
= ×
× ÷
÷ ×
× =
= +
+ =
= +
+ ×
× =
=
直接写得数.
0.36+0.4= 12÷40%= =
= =
=
1÷1%= 1﹣27.5%= =
= =
=
脱式计算(能简算的用简便方法计算,写出计算过程.)
(1)7.5×2.3﹣1.9×2.5
(2)(78.6﹣0.786×25+75%×21.4)×2011÷75
(3)1 +2
+2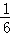 +3
+3 +4
+4 +5
+5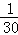
(4)9.1+9.2+9.3+…10.7+10.8+10.9.
直接写得数.
1.2÷ = 1÷0.01﹣1=
= 1÷0.01﹣1= ﹣
﹣ = 5÷
= 5÷ ×5=
×5=
2÷2%= 0.5﹣20= 5.7+11.8+4.3= 2 ﹣
﹣ +
+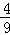 =
=
( +
+ )×24= 4.9×81=
)×24= 4.9×81=