看图填空：
已知：如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．求证：AD平分∠BAC．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠ADC=90°，∠EFC=90°（垂线的定义）
∴ =
∥
∴∠1=
∠2=
∵∠1=∠2（已知）
∴ =
∴AD平分∠BAC（角平分线定义）
某市根据2010年农林牧渔业产值的情况，绘制了如下两幅统计图，请你结合图中所给信息解答下列问题：
（1）2010年全市农林牧渔业的总产值为 亿元；
（2）扇形统计图中林业所在扇形的圆心角为 度（精确到度）；
（3）根据本地实际，市政府大力发展林业产业，计划2012年林业产值达60.5亿元，求这两年林业产值的年平均增长率．
袋子中装有三个完全相同的球，分别标有：“1”“2”“3”，小颖随机从中摸出一个球不放回，并以该球上的数字作为十位数；小颖再摸一个球，以该球上的数字作为个位数，那么，所得数字是偶数的概率是多少？（要求画出树状图或列出表格进行解答.）
解方程：
解不等式组
并把解集在数轴上表示出来．
计算：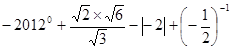
.