已知圆 的方程为:
的方程为: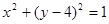 ,直线的方程为
,直线的方程为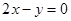 ,点
,点 在直线上,过点
在直线上,过点 作圆
作圆 的切线
的切线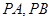 ,切点为
,切点为 .
.
(1)若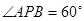 ,求点
,求点 的坐标;
的坐标;
(2)若点 的坐标为
的坐标为 ,过点
,过点 的直线与圆
的直线与圆 交于
交于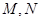 两点,当
两点,当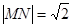 时,求直线
时,求直线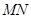 的方程;
的方程;
(3)求证:经过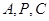 (其中点
(其中点 为圆
为圆 的圆心)三点的圆必经过定点,并求出所有定点的坐标.
的圆心)三点的圆必经过定点,并求出所有定点的坐标.
为了治理“沙尘暴”,西部某地区政府经过多年努力,到2009年底,将当地沙漠绿化了40%,从2010年开始,每年将出现这种现象:原有沙漠面积的12%被绿化,即改造为绿洲(被绿化的部分叫绿洲),同时原有绿洲面积的8%又被侵蚀为沙漠,问至少经过几年的绿化,才能使该地区的绿洲面积超过50%?(可参考数据lg2=0.3,最后结果精确到整数).
(1)在等比数列{an}中,a1+a2=324,a3+a4=36,求a5+a6的值;
(2)在等比数列{an}中,已知a3a4a5=8,求a2a3a4a5a6的值.
设数列{an}是等差数列,a5=6.
(1)当a3=3时,请在数列{an}中找一项am,使得a3,a5,am成等比数列;
(2)当a3=2时,若自然数n1,n2,…,nt,… (t∈N*)满足5<n1<n2<…<nt<…使得a3,a5, ,
, ,…,
,…, ,…是等比数列,求数列{nt}的通项公式.
,…是等比数列,求数列{nt}的通项公式.
已知等比数列{an}中,a3= ,S3=4
,S3=4 ,求a1.
,求a1.
某林场有荒山3 250亩,每年春季在荒山上植树造林,第一年植树100亩,计划每年比上一年多植树50亩(全部成活)
(1)问需要几年,可将此山全部绿化完?
(2)已知新种树苗每亩的木材量是2立方米,树木每年自然增长率为10%,设荒山全部绿化后的年底的木材总量为S.求S约为多少万立方米?(精确到0.1)