我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做旋转,这个定点称为旋转中心,旋转的角度称为旋转角.
(1)如图(1),△ABC经过旋转得到△DEF.试用直尺和圆规作出旋转中心(保留作图痕迹,不写作法);
(2)如图(2),正方形ABCD中,E、F分别为CD、AD的中点,连接BE、CF,△BCE按逆时针方向旋转后得到△CDF,则旋转中心为 (请在图中画出该点,标上字母,并回答),旋转的最小角度为 .
如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于点F,且BE=CF.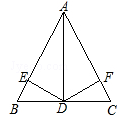
(1)求证:△BDE≌△CDF;
(2)求证:AD平分∠BAC.
在△ABC中,AB="13" cm,BC="10" cm,中线AD="12" cm.求证:△ABC是等腰三角形.
如图,等腰△ABC中,AB=AC,∠A=40°,线段AB的垂直平分线交AB于D,交AC于E,连接BE,求∠CBE的度数.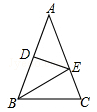
如图,C是AB的中点,AD=BE,CD=CE.求证:∠D=∠E.
利用网格线画图:如图,点A、B、C都在正方形网格的格点上.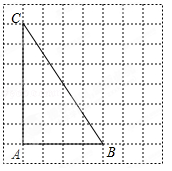
(1)在BC上找一点P,使PA=PB;
(2)在BC上找一点Q,使点Q到AB和AC的距离相等.