如图,在△ABC中,AB=AC,AD⊥AB点D,BC=10cm,AD=8cm,点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0)。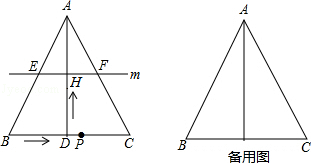
(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;
(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;
(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值,若不存在,请说明理由。
已知:A=x3-2y3+3x2y+xy2-3xy+4, B=y3-x3-4x2y-3xy-3xy2+3,C=y3+x2y+2xy2+6xy-6.试说明无论x.y取何值A+B+C都是常数
如果a、b互为相反数,c、d互为倒数,m的绝对值等于5,求3cd-|a+b|-m的值.
如图,在△ABC中,∠1=∠2,∠3=∠4,∠A=60°,求证:CD+BE=BC.
、如图所示,在△ABC中,∠C=90°, AD是∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF.
证明:(1)CF=EB.(2)AB=AF+2EB
如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.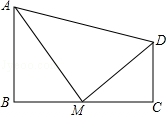
求证:(1)AM⊥DM;(2)M为BC的中点.