已知命题p：m<0，命题q：∀x∈R，x2＋mx＋1>0成立，若“p∧q”为真命题，则实数m的取值范围是
| A．[－2，0] |
| B．(0，2) |
| C．(－2，0) |
| D．(－2，2) |
已知命题p：“∀x∈R，∃m∈R，使4x＋2x·m＋1＝0”．若命题p为真命题，则实数m的取值范围是
| A．(－∞，－2] |
| B．[2,+∞) |
| C．(－∞，－2) |
| D．(2,+∞) |
已知命题p：∃x∈[0，
]，cos2x＋cosx－m＝0的否定为假命题，则实数m的取值范围是( )
A．[－ ，－1] |
| B．[－，2] |
| C．[－1,2] |
| D．[－，＋∞) |
已知命题p：“∀x∈[1,2]，x2－a≥0”；命题q：“∃x∈R，x2＋2ax＋2－a＝0”．若命题“p且q”是真命题，则实数a的取值范围为( )
| A．a≤－2或a＝1 |
| B．a≤－2或1≤a≤2 |
| C．a≥1 |
| D．－2≤a≤1 |
=（）
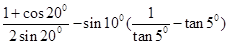A． |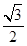
B． |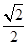
| C．1 |
| D．2 |
中，若
，则
与
的等比中项为（ ）
