如图所示,已知在平行四边形ABCD中,BE=DF.求证:AE=CF.
解方程: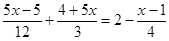
据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”,为了缓解供电需求紧张矛盾,某市电力部门于本月初统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:
| 时间 |
换表前 |
换表后 |
|
| 峰时(8:00~21:00) |
谷时(21:00~次日8:00) |
||
| 电价 |
每度0.52元 |
每度0.55元 |
每度0.30元 |
(1)小张家上月“峰时”用电50度,“谷时”用电20度,若上月初换表,则相对于换表前小张家的电费是增多了还是减少了?增多或减少了多少元?请说明理由.
(2)小张家这个月用电95度,经测算比换表前使用95度电节省了5.9元,问小张家这个月使用“峰时电”和“谷时电”分别是多少度?
已知,如图,B,C两点把线段AD分成2∶5∶3三部分,M为AD的中点,BM=6cm,求CM和AD的长.
为了进一步落实“节能减排”措施,冬季供暖来临前,某单位决定对9000平方米的“外墙保温”工程进行招标,现有甲、乙两个工程队参与投标,比较这两个工程队的标书发现:乙队每天完成的工程量是甲队的1.5倍,这样乙队单独干比甲队单独干能提前15天完成任务.问甲队每天完成多少平方米?
先化简,再求值: ,其中
,其中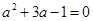 .
.