设实数
，有如下四个结论：
①若
则
；②若 则
；
③若
则；④若 则．
则下列命题成立的是（ ）
| A．①④ | B．②③ | C．①③ | D．②④ |
设直线
（m为常数），圆
，则
| A．当m变化时，直线l恒过定点(-1，1); |
| B．直线l与圆C有可能无公共点 |
| C．若圆C上存在关于直线l对称的两点，则必有m=0 |
D．若直线 与圆C有两个不同交点M、N，则线段MN的长的最小值为 |
若实数x,y满足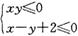
，则
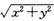的最小值为
| A．O | B． |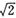
C．2 | D．4 |
已知平面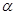
//平面β，点
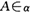，直线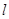
经过点A，则“
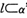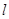”是“//β"的
| A．充要条件 | B．充分不必要条件 |
| C．必要不充分条件 | D．既不充分也不必要条件 |
要使函数
在点x= -1处连续，则对f(x)可以补充的一个条件是
A．当x="-1" 时， |
B．当x="-1" 时， |
| C．当x=l时， |
D．当 x=1 时， |
已知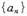
是等比数列，
，则该数列前6项之积为
| A．8 | B．12 | C．32 | D．64 |