由于工业化城镇化的推进,大气污染日益加重,空气质量逐步恶化,雾霾天气频率增大,大气污染可引起心悸、胸闷等心脏病症状.为了解某市患心脏病是否与性别有关,在某医院心血管科随机的对入院50位进行调查得到了如表:
| |
患心脏病 |
不患心脏病 |
合计 |
| 男 |
20 |
5 |
25 |
| 女 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
参考临界值表:
| p(p2≥k) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| K |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式:K2= 其中n ="a" +b +c +d).
其中n ="a" +b +c +d).
问有多大的把握认为是否患心脏病与性别有关.答:( )
A.95% B.99% C.99.5% D.99.9%
设A1,A2是椭圆 +
+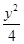 =1的长轴两个端点,P1,P2是垂直于A1A2的弦的端点,则直线A1P1与A2P2交点的轨迹方程为( )
=1的长轴两个端点,P1,P2是垂直于A1A2的弦的端点,则直线A1P1与A2P2交点的轨迹方程为( )
A. + +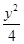 =1 =1 |
B.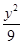 + + =1 =1 |
C. - -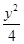 =1 =1 |
D.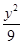 - - =1 =1 |
已知点M(-3,0),N(3,0),B(1,0),动圆C与直线MN切于点B,过M、N与圆C相切的两直线相交于点P,则P点的轨迹方程为( )
A.x2-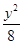 =1(x>1) =1(x>1) |
B.x2-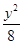 =1(x<-1) =1(x<-1) |
C.x2+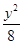 =1(x>0) =1(x>0) |
D.x2-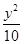 =1(x>1) =1(x>1) |
设F(1,0),M点在x轴上,P点在y轴上,且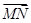 =2
=2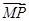 ,
,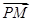 ⊥
⊥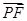 ,当点P在y轴上运动时,点N的轨迹方程为( )
,当点P在y轴上运动时,点N的轨迹方程为( )
| A.y2=2x | B.y2=4x |
C.y2=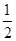 x x |
D.y2= x x |
设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( )
A. - - =1 =1 |
B. + + =1 =1 |
C.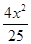 - - =1 =1 |
D.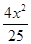 + + =1 =1 |
已知M(-2,0),N(2,0),则以MN为斜边的直角三角形的直角顶点P的轨迹方程为( )
| A.x2+y2=2 | B.x2+y2=4 |
| C.x2+y2=2(x≠±2) | D.x2+y2=4(x≠±2) |