通过随机询问100名性别不同的大学生是否爱好踢毪子运动，得到如下的列联表：
| |
男 |
女 |
总计 |
| 爱好 |
10 |
40 |
50 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
30 |
70 |
100 |
附表：
| P（K2≥k） |
0.10 |
0.05 |
0.025 |
| k |
2.706 |
3.841 |
5.024 |
随机变量
，经计算，统计量K2的观测值k≈4.762，参照附表，得到的正确结论是（ ）
A.在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别无关”
C.有97.5%以上的把握认为“爱好该项运动与性别有关”
D.有97.5%以上的把握认为“爱好该项运动与性别无关”
已知两条直线l1：（a﹣1）x+2y+1=0，l2：x+ay+3=0平行，则a=（）
| A．﹣1 | B．2 | C．0或﹣2 | D．﹣1或2 |
直线l与圆x2+y2+2x﹣4y+a=0（a＜3）相交于A，B两点，若弦AB的中点C为（﹣2，3），则直线l的方程为（）
| A．x﹣y+5=0 | B．x+y﹣1=0 | C．x﹣y﹣5=0 | D．x+y﹣3=0 |
直线y=x+m与圆x2+y2=16交于不同的两点M，N，且|
|≥
|
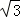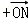|，其中O是坐标原点，则实数m的取值范围是（）
A．（﹣2 ，﹣]∪[，2） |
| B．（﹣4，﹣2]∪[2，4） |
| C．[﹣2，2] |
| D．[﹣2，2] |
若顶点在原点，始边为x轴的非负半轴的钝角α的终边与圆x2+y2=2相交于A（x1，y1），射线OA绕点O顺时针旋转30°后，与圆x2+y2=2相交于B（x2，y2），当|x1﹣x2|有最大值时，cosα=（）
A． |
B． |
C． |
D． |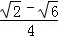
在下列直线中，与非零向量
=（A，B）垂直的直线是（）
A.Ax+By=0 B.Ax﹣By=0 C.Bx+Ay=0 D.Bx﹣Ay=0